Electrostatics: Coulomb's Law
Finding the magnitude of the force between two charges
Given two point charges, each exerts a force on the other with a magnitude given by Coulomb's Law: \begin{equation}\label{Coul} F=k\frac{Qq}{ r ^2} \tag{10.1}\end{equation} where $Q$ and $q$ are the magnitudes of the two charges, $r$ is the distance between them, and $k$ is a constant, sometimes written $k = \frac{1}{4\pi\epsilon_0}$ where $\epsilon_0$ is the permittivity of free space. The permittivity of free space will come up again later, but for now, don't worry about it. We'll use $k$. $$ k = 9 \times 10^9 \frac {\mbox{Nm}^2}{\mbox{C}^2} $$
Equation 10.1 gives the magnitude only. To get the direction, for now, simply look at the two charges and determine whether they have the same or opposite charge. If they are the same (either both positive or both negative), then they repel and they arrows point away, like so: If they are opposite, then they attract and the arrows point toward each other, like so: Then you just look at the arrow, and determine the components or angle as you would for any other vector.
Visualizing Coulomb's Law
We've done several examples now, but to give you a feel for how I visualize Coulomb's Law, try this flash demo.
You should see two charges--one red (negative) and one blue (positive)--and a force arrow.
You can click and drag on the charge with an arrow to see how the force (magnitude and direction) changes based on distance away and direction from the other charge.
You can also double click to change the sign (color) of the charge. Give it a try. And refer back to it when you do the examples.
Now that you have a conceptual understanding, let's start with an example in 1D.
- Find the force on the $3$ C charge.
- Find the force on the -4 C charge.
- What if the same charges were moved so that they were 3m apart?
Solution: For part a) Let's say $Q$ is the 3C charge and $q$ is the 4C charge. Then $r=6$ m. (If that's not obvious, look at the diagram.) To get the magnitude of the force, we just plug in.

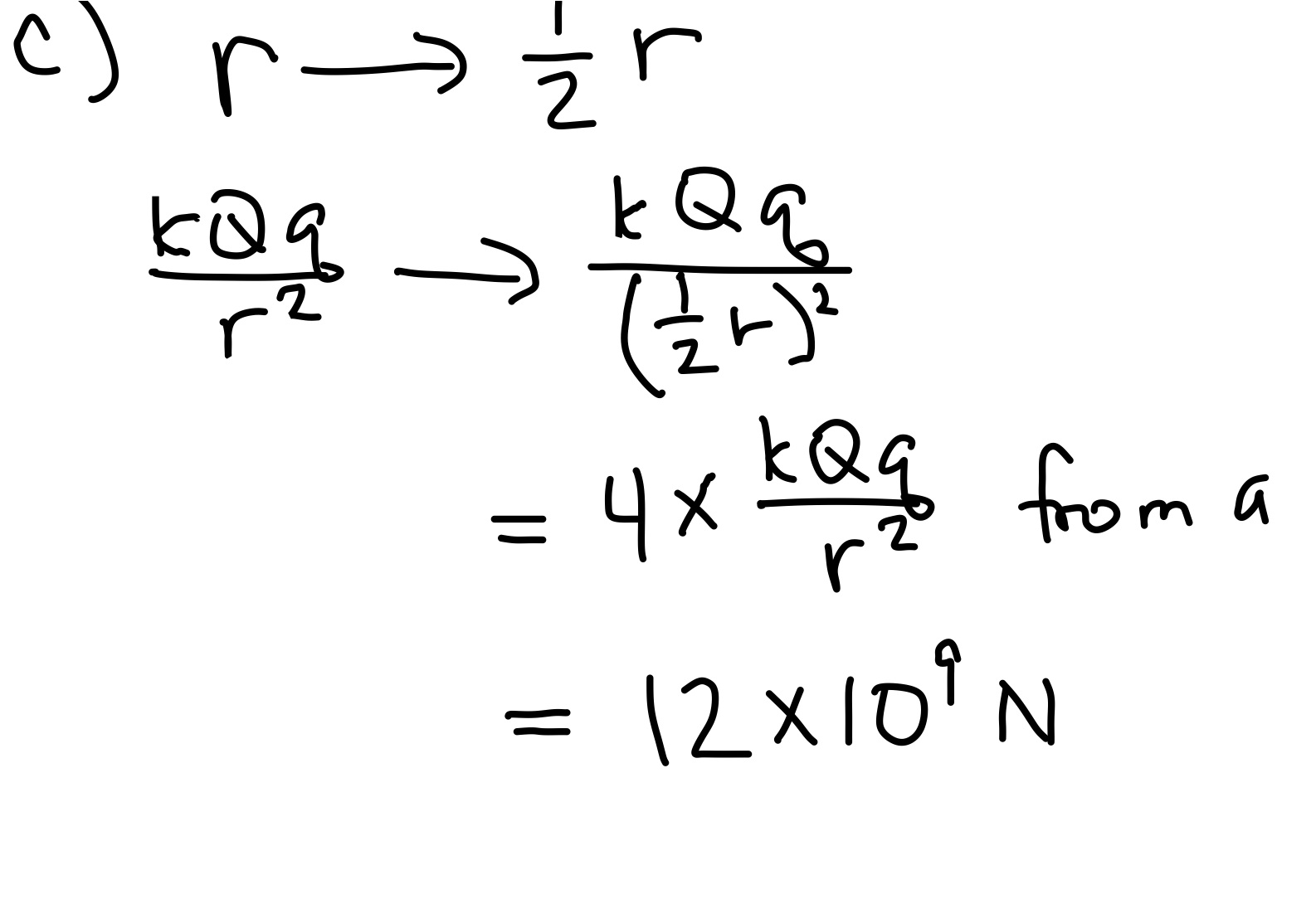
We didn't need to do any calculations for part b). That's because nothing about the magnitude changes by changing the order of multiplying 3$\cdot$4 or 4$\cdot$3. The direction changes. Because the two charges have opposite signs, they attract each other. The force on the 3C is in the negative $x$ direction, and the force on the -4C charge is in the positive $x$ direction. (The force arrows point toward each other, attracting.) You also could have done part b) by realizing that the two forces are a Newton's Third Law-pair; therefore the forces on the two charges must be equal and opposite.
And an example in 2D:
Example 2: Two charges are fixed in position as shown below: A 2C charge at (2,0)m and a -3C charge at (5,3)m. Find the force on the -3C charge.
Solution: Calculating the magntitude is straightforward. Just plug the magnitudes into Coulomb's Law. $$ F = k\frac{Qq}{ r ^2}$$ $r$ is the distance between the two charges. You can use the pythagorean theorem to get that $r^2 = 3^2 + 3^2 = 18m^2$ $$ F = (9\times 10^9 \frac{Nm^2}{C^2}) \frac{(2C)(3C)}{ 18m^2} = 3\times 10^9 N $$ To figure out the direction, you again just look at the arrow. The charges attract, so the force is directed along the line between the two charges and toward the other charge. You probably know it's a 45$^\circ$ angle, but in case you didn't, you would use $\tan\theta = \frac{-3m}{-3m}$ depending on how smart your calculator is, that will return either 45$^\circ$ or 225$^\circ$. The correct answer is $\vec F = 3\times 10^9 N @ 225^\circ$.
(If your calculator returned 45$^\circ$, you will need to look at a picture whenever you give an angle like that. You can see the force arrow goes down and to the left, whereas a 45$^\circ$ angle would be up and to the right.)
Notice that our answers to the last example are extremely large. The numbers I chose are not terribly realistic; I just wanted to start with nice round numbers. However, most charges that we measure are on the order of $\mu$C (10$^{-6}$C) or nC (16$^{-9}$C) or even smaller.
Coulomb's Law and Newton's Law of Universal Gravitation
You might have noticed the similarity in form to Newton's Law of Universal Gravitation which states that $$ F = G\frac{Mm}{r^2} $$. The two equations have the same form $$ F = (\mbox{constant})\frac{\mbox{(property of object 1)(property of object 2)}}{\mbox{(the distance between them)}^2}$$
Solution: Electrons have mass $m_e = 9.1 \times 10^{-31}$kg and charge (magnitude) $ e = 1.6 \times 10^{-19}$C. Therefore:

It might surprise you to learn that the electric force is on the order of $10^{42}$ times stronger! Gravity is far and away the weakest of the four fundamental forces.
Putting it all together: magnitude and direction in one equation
It is possible to write Coulomb's Law in a way that includes direction, but it looks significantly more complicated. For the beginning student, I recommend the method we've been using: simply look at the charges and determine the direction depending on whether the charges attract or repel each other.Coulomb's Law in vector form
$$ \vec F = k \frac{Qq}{r^2} \hat r $$ where $\hat r$ is the unit vector that points in the direction from $q$ to $Q$. (Recall that a unit vector has magnitude of one, so multiplying by a unit vector does not change the magnitude of the force; it simply tells you the direction.) When you use this equation, you must also include the signs for the charges. Notice that if both charges are positive or negative, the direction of $\hat r$ is unchanged. But of course if they are opposite signs, the direction of $\hat r$ will flip. This will take into account that like charges repel and opposites attract.
Principle of Superposition
What do you do if you have more than two charges?
Let's say you have four charges and you want to calculate the electrostatic (Coulomb) force on one of them, let's call that one $Q$, due to the other three, let's call them $q_1$, $q_2$, and $q_3$. You simply calculate the three forces on $Q$ using Coulomb's Law for each pair of charges ($F_1 = k\frac{Q q_1}{r^2}$, $Q q_2$, and $Q q_3$), and then add up all three of those forces. Don't forget that each of those forces is a vector!Example Four charges are located at the corners of a rectangle which is 40cm by 30cm. The top two charges are $+1\mu$C and the bottom two charges are $-2\mu$C. Find the force on the top-right $1\mu$C charge.
Solution
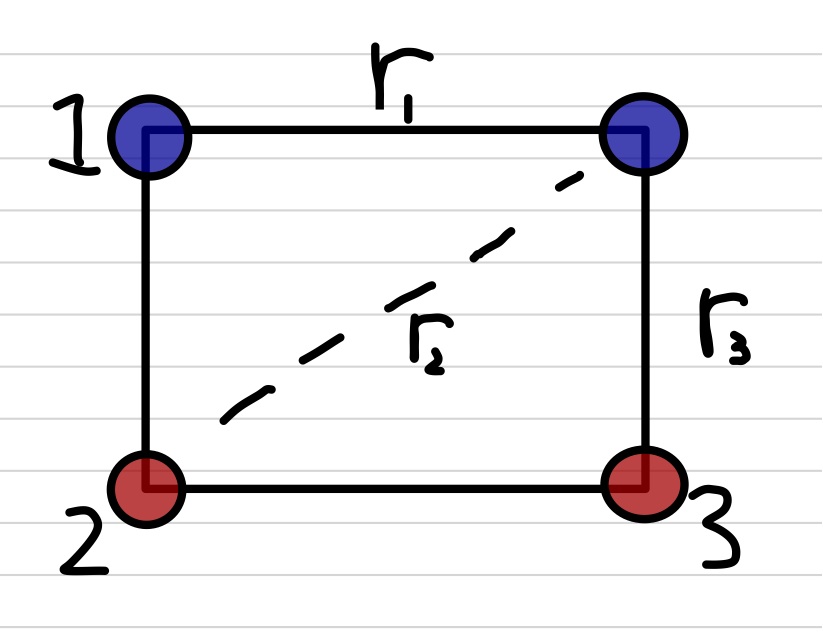
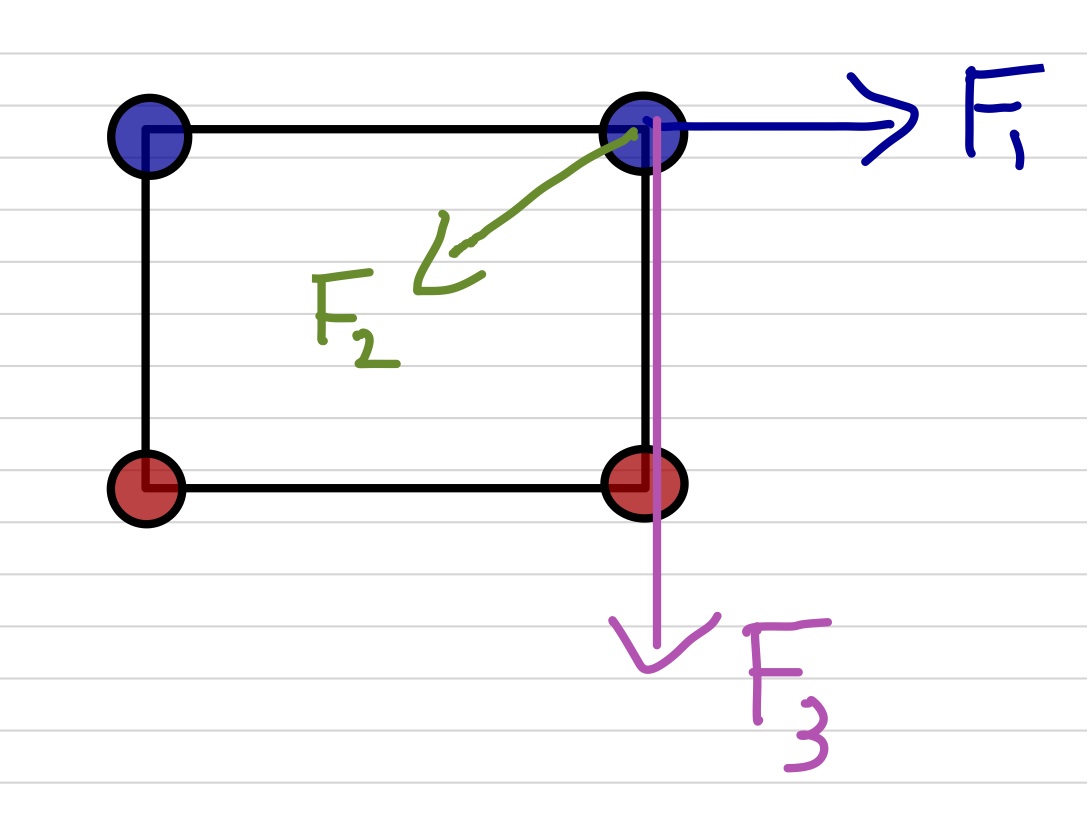

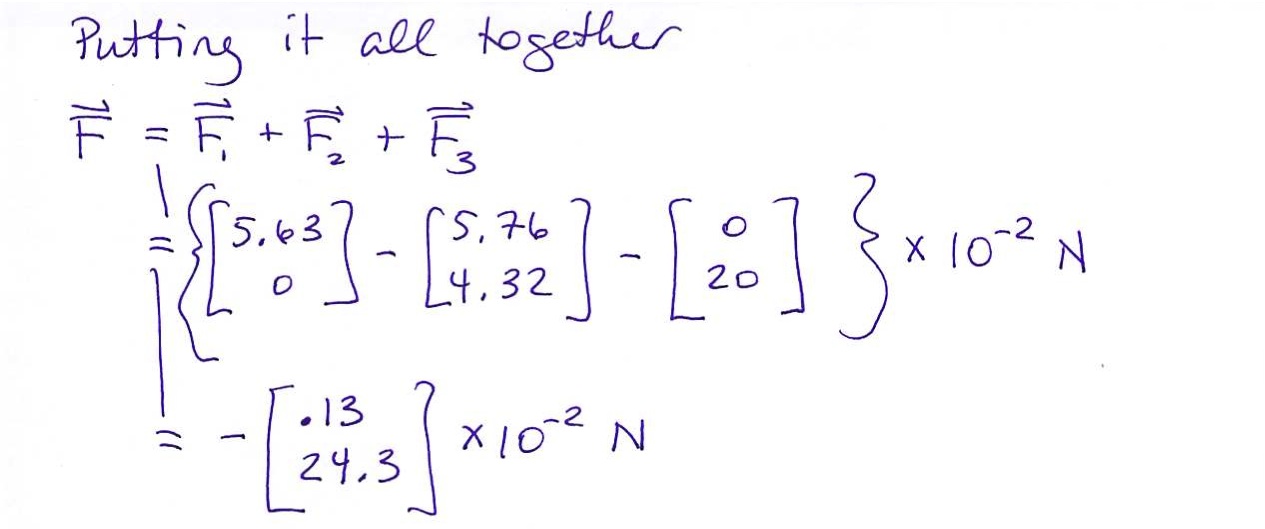
Let's do this more formally
The force, $\vec F$, on charge $Q$ due to $n$ other charges, $q_1$, $q_2$, $\ldots$, $q_n$ is given by: \begin{eqnarray*} \vec F &=& \vec F_1 &+& \vec F_2 &+& \ldots &+& \vec F_n \\ \vec F &=& k\frac{Q q_1}{r_1^2}\hat r_1 &+& k\frac{Q q_2}{r_2^2}\hat r_2 &+& \ldots &+& k\frac{Q q_n}{r_n^2}\hat r_n \\ \vec F &=& \displaystyle\sum_{i=1}^n k\frac{Q q_i}{r_i^2}\hat r_i \end{eqnarray*}
And that is the general equation for finding the force on one charge, $Q$, due to several other charges.