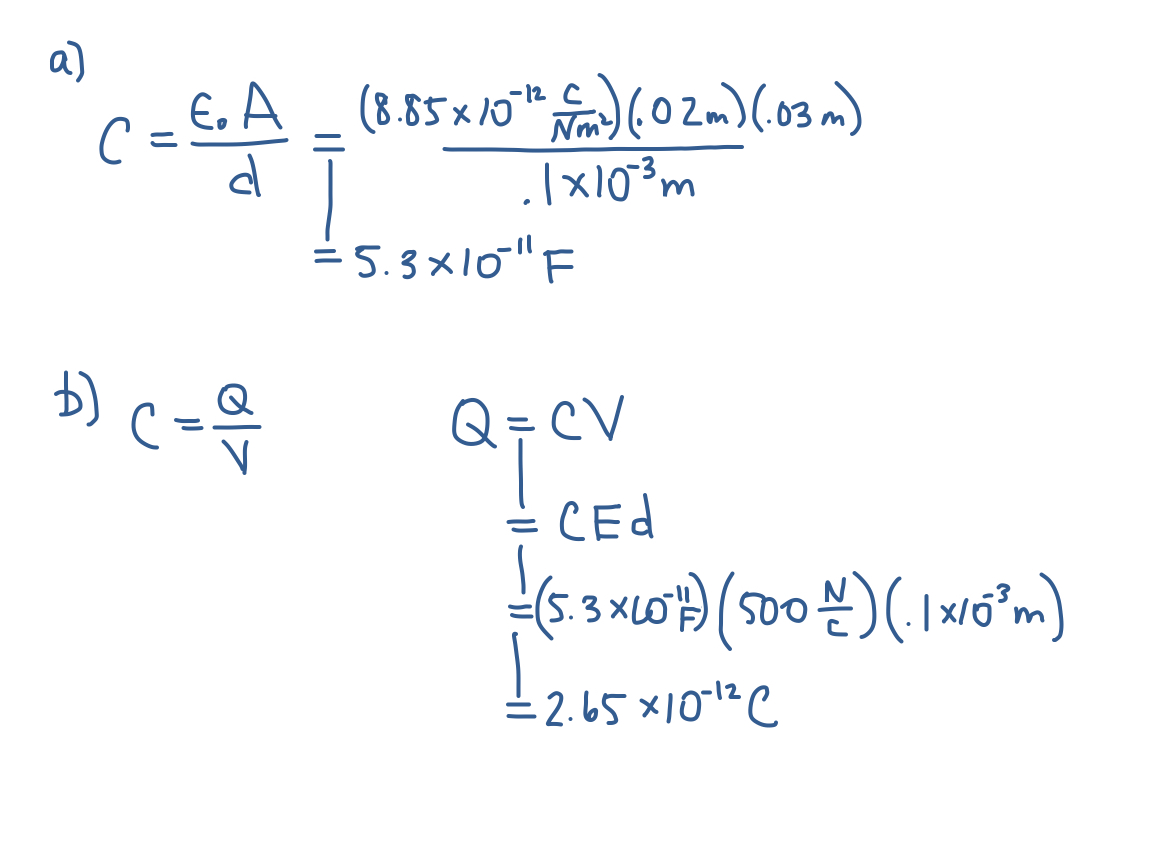Electrostatics: Capacitance
Capacitors are used to store energy. In this section, I'll talk about the basics, and we will return to capacitors again when we talk about circuits.
A capacitor is made of two conductors. Capacitance is defined as the magnitude of the charge on each conductor divided by the potential difference between the two conductors. $$C = \left| \frac{Q}{V} \right| $$
Capacitance has units of Farads, F, where one Farad is equal to a Coulomb over a Volt, F=$\frac{\mbox{C}}{\mbox{V}}$.
The great thing is, you don't have to worry about the sign of anything. Capacitance is always positive, so you can just check and fix the sign at the end.
There are three configurations of capacitors that are commonly used: parallel plates, concentric cylinders, and concentric spheres. Let's start by deriving the form of the capacitance for a parallel plate capacitor.
Parallel Plate Capacitor
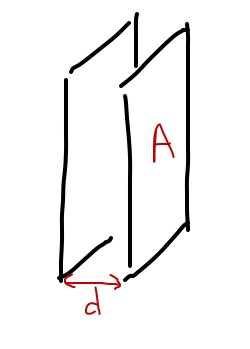Imagine two conducting plates with surface area of $A$ and separation distance, $d$. As we will see, that's all the information we need to know to define the capacitance for a parallel plate capacitor.
Let's use what we have found about the electric field from an infinte sheet and find the capacitance, $C$.
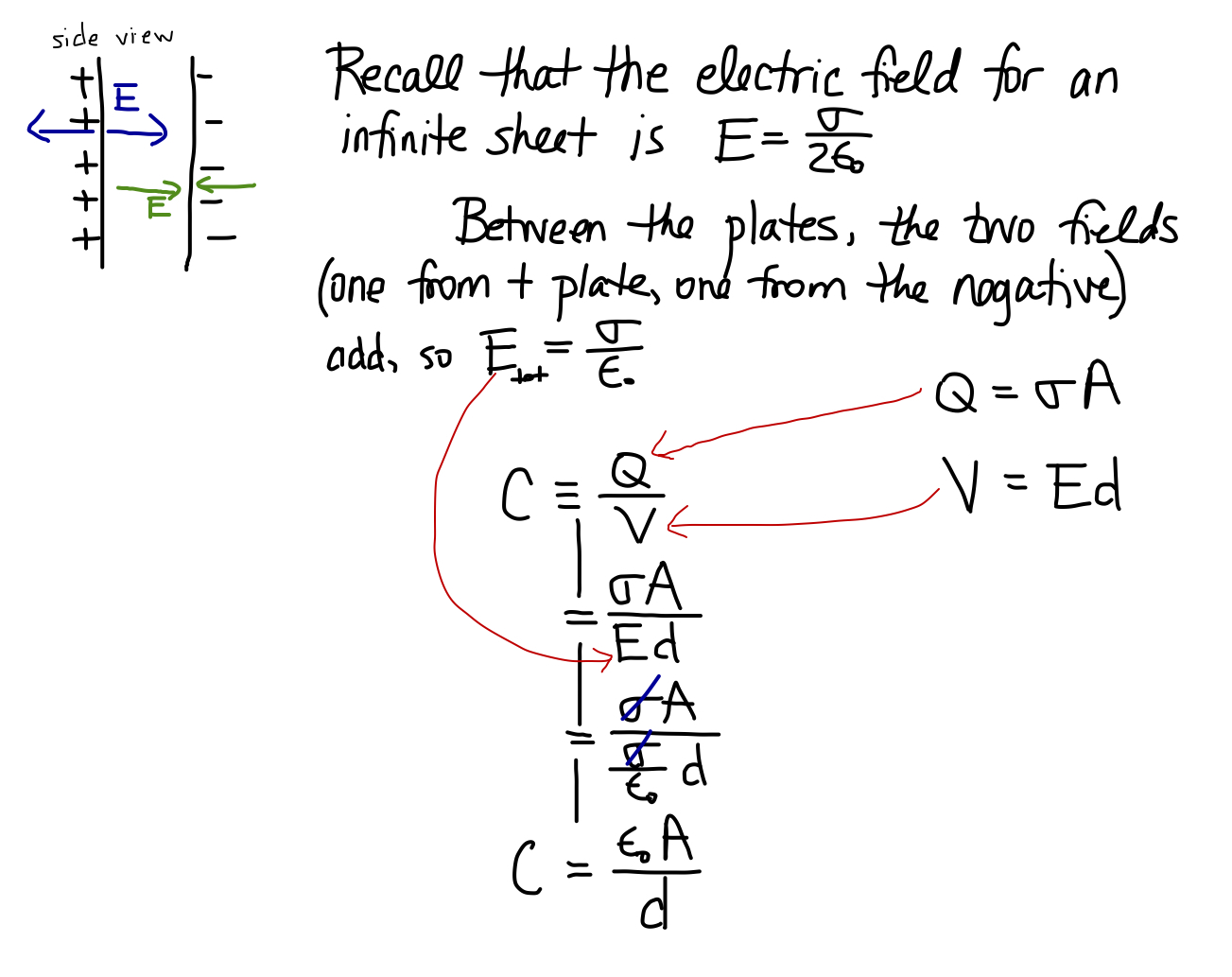
For a parallel plate, $$C=\frac{\epsilon_0A}{d}$$ where $A$ is the area of one plate and $d$ is the separation between the plates.
Notice that the capacitance depends only on the geometry of the configuration--no dependence on charge, only the area and separation of the plates. The charge will cancel for all capacitance--this is because the potential difference is proportional to the charge on the plates. In all cases, the capacitance depends only on the geometry of the situation.
Let's do an example.
Example: A parallel plate capacitor is made of metal plates with area 2cm by 3cm and a separation distance of 0.1mm.
- Find the capacitance of this arrangement
- If the electric field between the plates is 500 N/C, what is the magnitude of the charge on each plate?
Answer
